The brief was to visualise a journey through the neural network of creativity. This involved a lot of spline modelling and layering in order to arrive at a desired level of complexity while also being able to blend between states. Here, the very root processes will be discussed that helped in making the actual assets on this title sequence.

Spline modelling and animating:

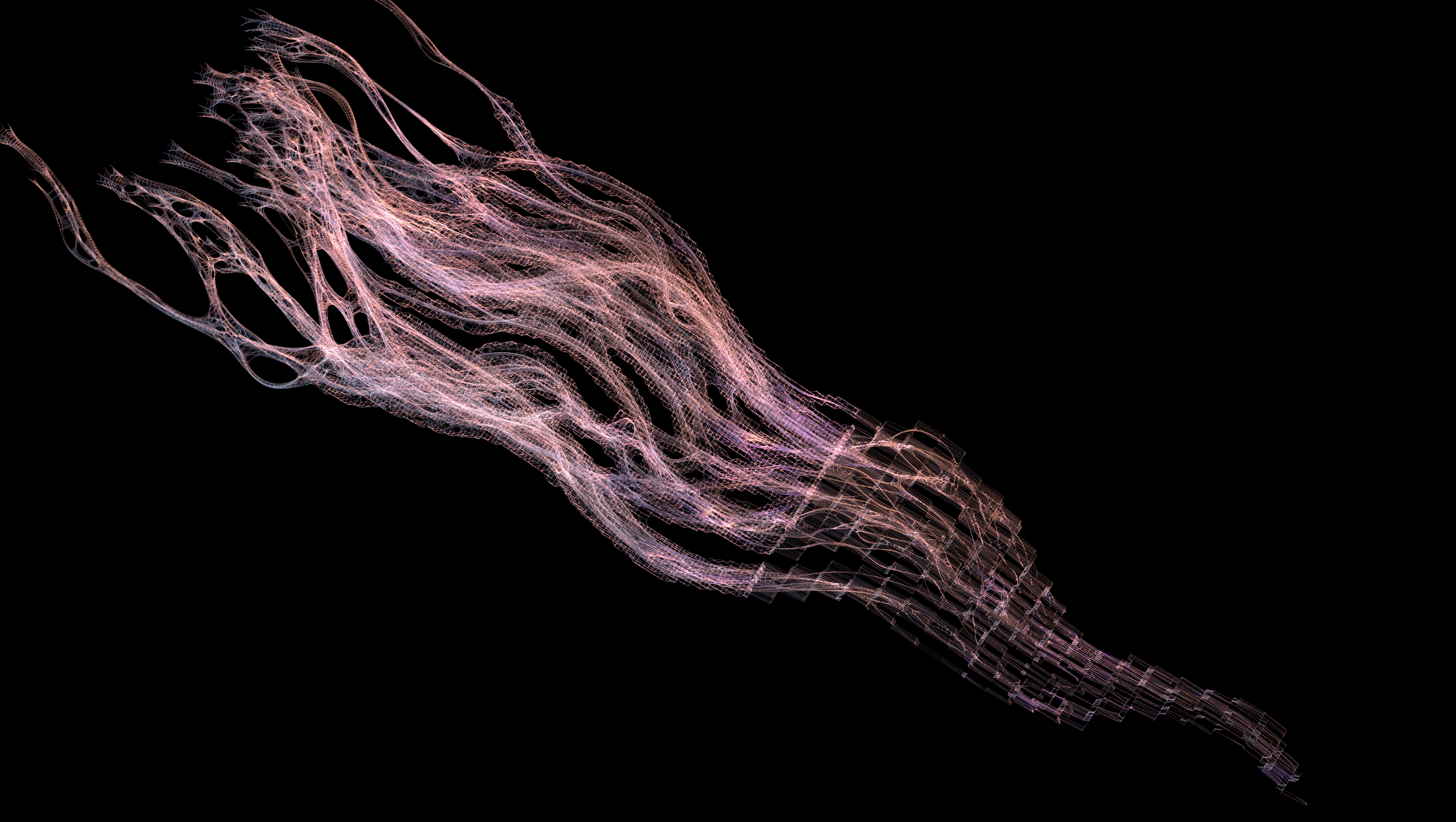
This spline animation summarises the crux of all the procedures that are performed to be able to manipulate any given curves going towards a destination. The flexibility lies in being able to blend between states like here the 'splitting' of the line is basically lots of curves blending between the central line and the final bulged out curves.
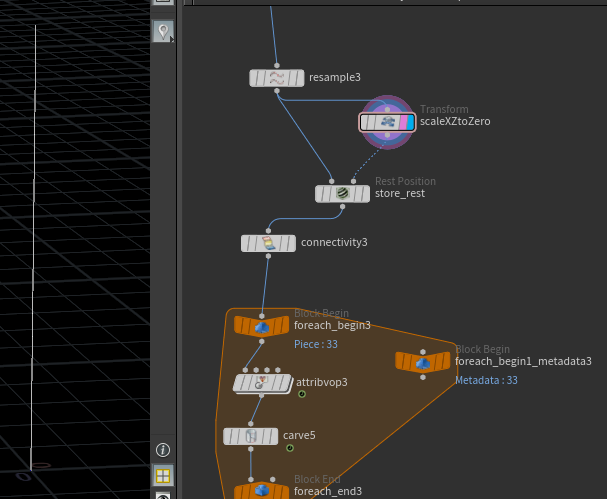
The above two images show the two main states between which all the curves are blending. To control the blending, the curves' UVs can be used from resample node's 'curveu' attribute as a driving parameter for the ramp. This will let the user decide what portion of the curve blends at what state.
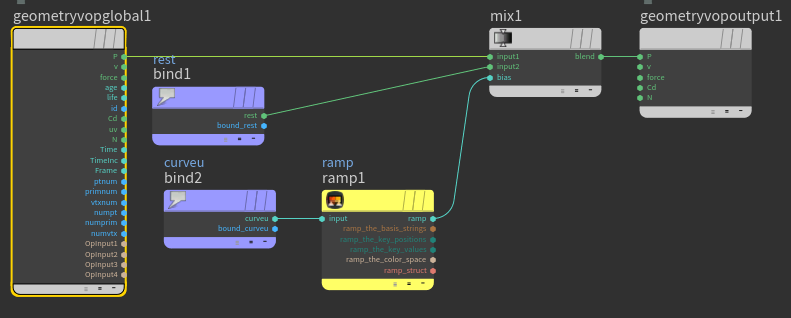
This is the blending VOP. Understand it as a hugely generalised approach for any curve based effects where irrespective of length, the effect can be manipulated by combining ramps driven through the curve's UVs. The rest position is the second state where all the curves merge into one spline.
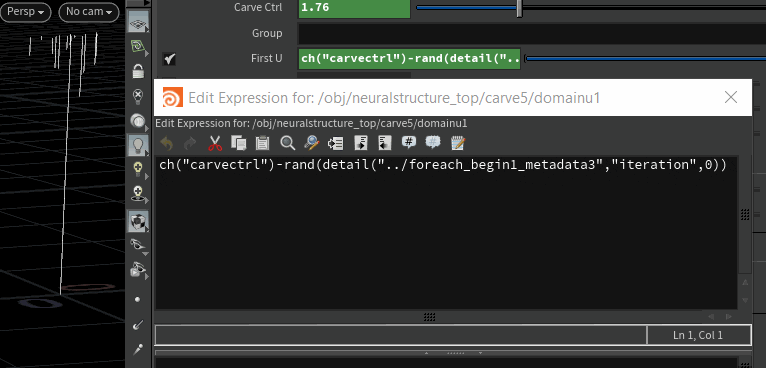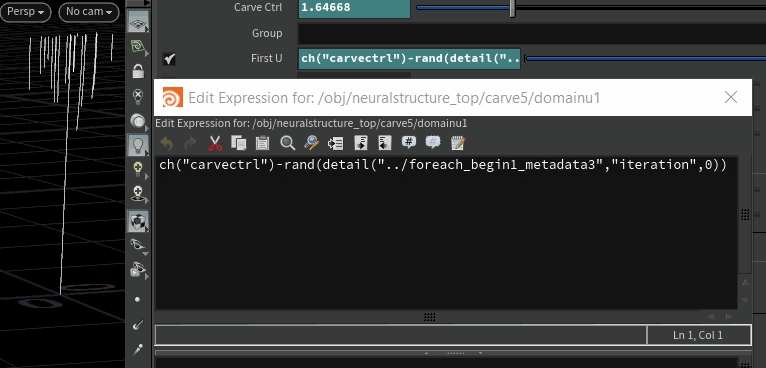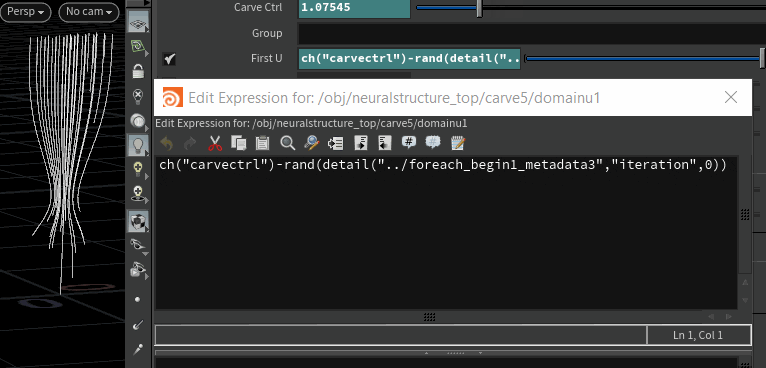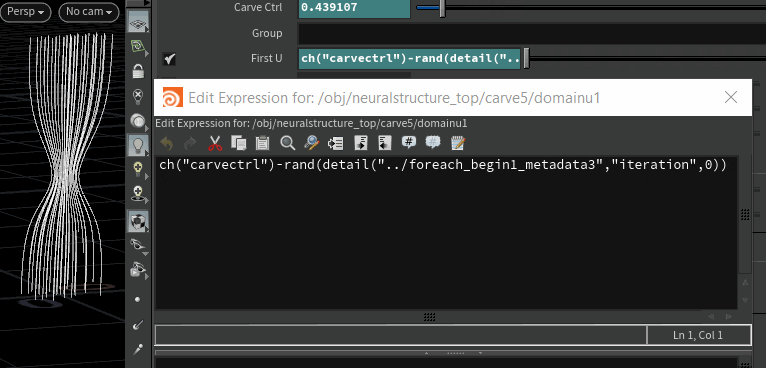
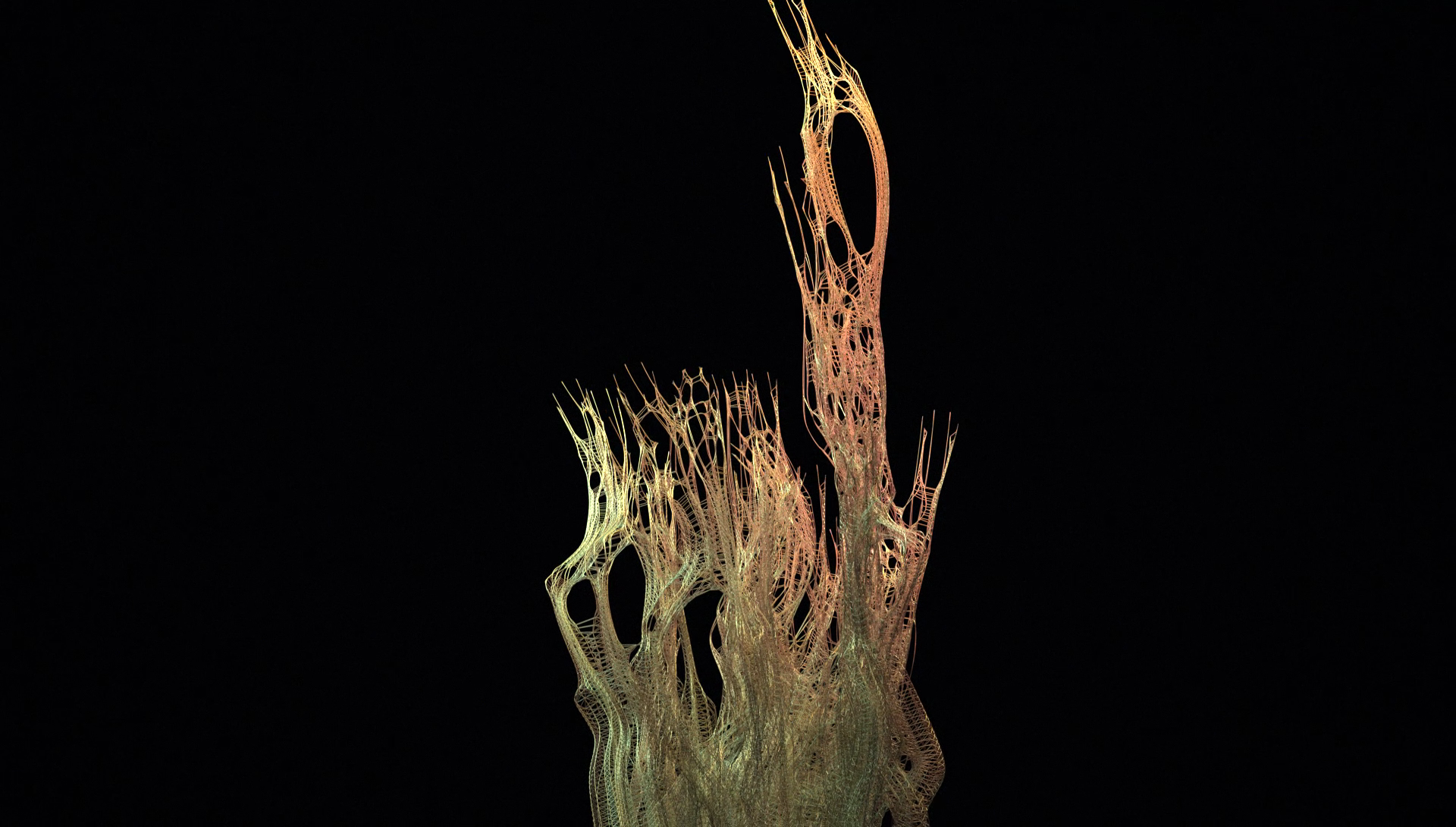
This can arguably be done using particles and trails but this approach lets you go into modelling first and then have more control over how each curve gets completed. So this is a standard Carve SOP running in a for-each connected piece loop that can take any number of given curves and then animate them carving individually with slight offset. The 'Carve Ctrl' parameter is a float param added in the parameter interface as a control.
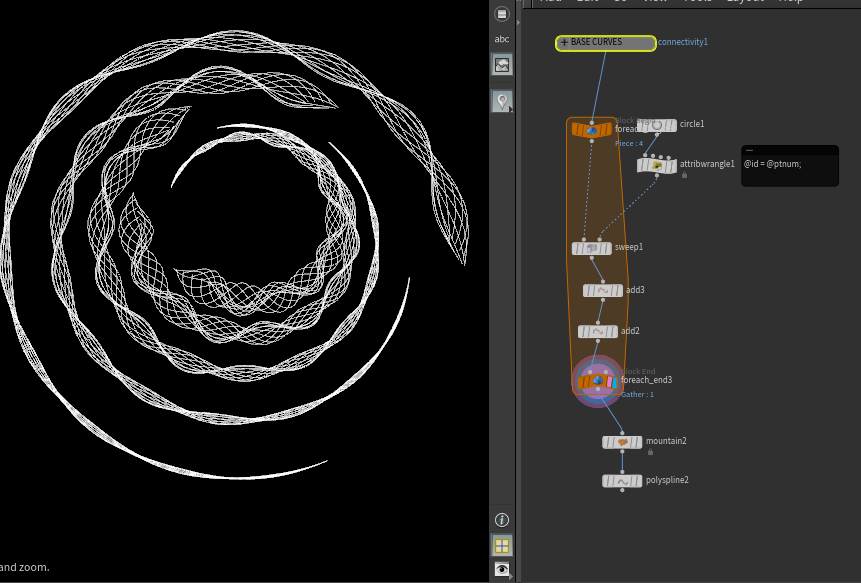
This is another simple yet elegant approach towards modelling splines spinning or twisting around a given number of curves. The new Sweep node from H18 is a powerful way to maintain UVs and also manipulate scaling, pitch, yaw and roll in order to get a spun up tube going along splines. Once the tube geo isderived from sweep, the add node can delete prims but keep points that can then be connected as curves if they have an id attribute as shown from an earlier wrangle. The other way is to use parallel transport attributes like tangents and normals and to push out the input curve along its own normals (that can be rotated based on iteration number to get a 'tube' of curves around a curve).
Using the above three simple processes: curves with blend states, individual carving with offset and splines around splines; a great layered effect like this one can be achieved:

Microchip-like distribution:
While referring to this resource, it was essential to understand that a complex distribution can be derived without having too much high frequency variations. That is why, a simple noise driven ramp can be used compounded with layering to arrive at a significantly complex yet believable pattern. This one was art directed for the title sequence but also to keep the polycount in check. A great way to push this effect further is by having huge amount of very small scaled elements along side the very few large elements. The Chebyshev Worley F1 noise can be used to derive good distribution of scale and density across a grid.

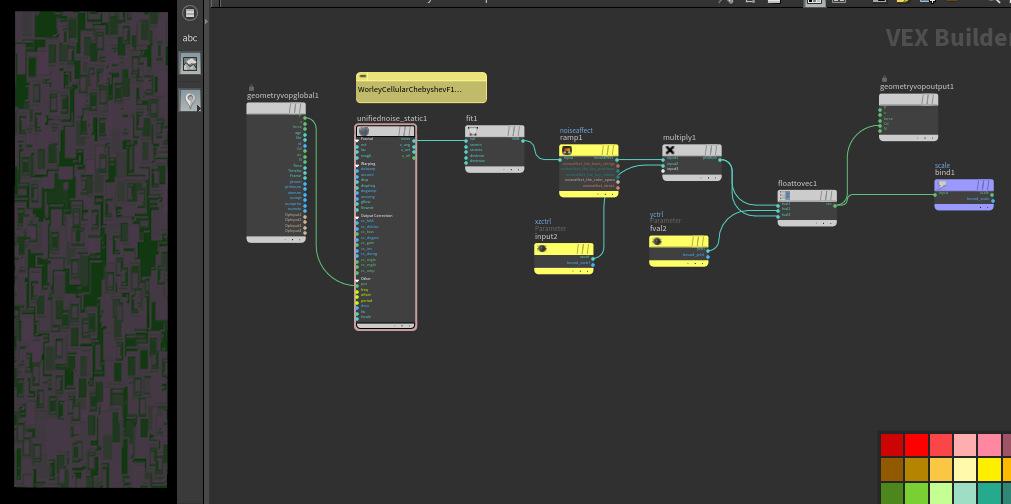

A good distribution when layered well can give a great illusion of detail:


